The C programming language is a compiled language, no wonder when you type gcc main.c a compilation process starts. This command tells the computer to start Compiling a C program and a lot goes behind the scene. In this article, I'm going to discuss what goes behind the hood during the C compilation process of a C program.

Introduction

Lets get the bare basics. C programming language is a high-level language and it needs a compiler to convert it's code into an executable code so that the program can be run on our machine. Its like this, the machine does not understand the C codes. Humans do not understand the machine code (I can feel guru programmers murmuring - ok, fine maybe not all humans). So, to make everyone involved happy, we need to balance things up. Thats where C program compilation comes in by running the C code through the gcc compiler, which in turn generates an executable file that can be run by the computer and understandable by humans, yeah....now, all humans.

Alas! wait a sec right there. Are you for real? Is C really a high-level language? Well, if I was asked nicely, I would say C is a high level language. Considered high-level because they are closer to human languages and further from machine languages. High level: easy to understand by programmer/human(user friendly). Middle level: less easy to understand by programmer(less user friendly). Low level: very hard to understand by programmer but piece of cake for computer(computer friendly). Afterall, the compiler does the rest of the job. We(programmers) only write the codes in IDE-user-friendly kind of way, after that, gcc all the way. The middle and low level stuffs happen during compilation. But, whichever one you think it should be, you're right, right so because C does it all.

Now, back to our introduction, the GNU Compiler Collection (GCC) is a set of compilers collection for various languages such as ada, C, C++, fortran, ObjC, ObjC++, at one point java e.t.c. Be careful not to confuse GCC for abbreviation of Gulf Cooperation Council. GCC is distributed under the GNU free software license. By the way, if you are an eagle eye reader like I am, you should have noticed the G in GNU of the GCC abbreviation. GNU is a recursive acronym for "GNU is Not Unix!", chosen because GNU's design is Unix-like, but differs from Unix by being free software and containing no Unix code.

Let me put it straight; GNU is just like Unix but it is NOT, it is Linux system, Linux is the kernel component. Period! The rest of the system consists of other programs, many of which were written by or for the GNU Project.

Behind the Scene

Behind the scene a lot happens actually. The programmer writes C codes and runs the codes through the gcc compiler like I mentioned earlier. And......Viola! This happens.....

Confused? Think we must be in the Crude Oil Refinery?

Far from it. If anything, we must be in the stone age counting our money. So relax, fasten your seat belt and let me take you on an electric ride. Actually, when I first heard of it, I was more confused than you really are right now. But I bet you, we're not in the crude oil distillation unit, so it's not a crude oil refining process to bring some generous grub of mucus called "crude" to boiling point in order to extract petrol or diesel from its broken components; neither is it the catalytic conversion of solar to chemical energy on some plasmonic metal nanostructures. Let me explain what the diagram illustrates.

Preprocessor Stage

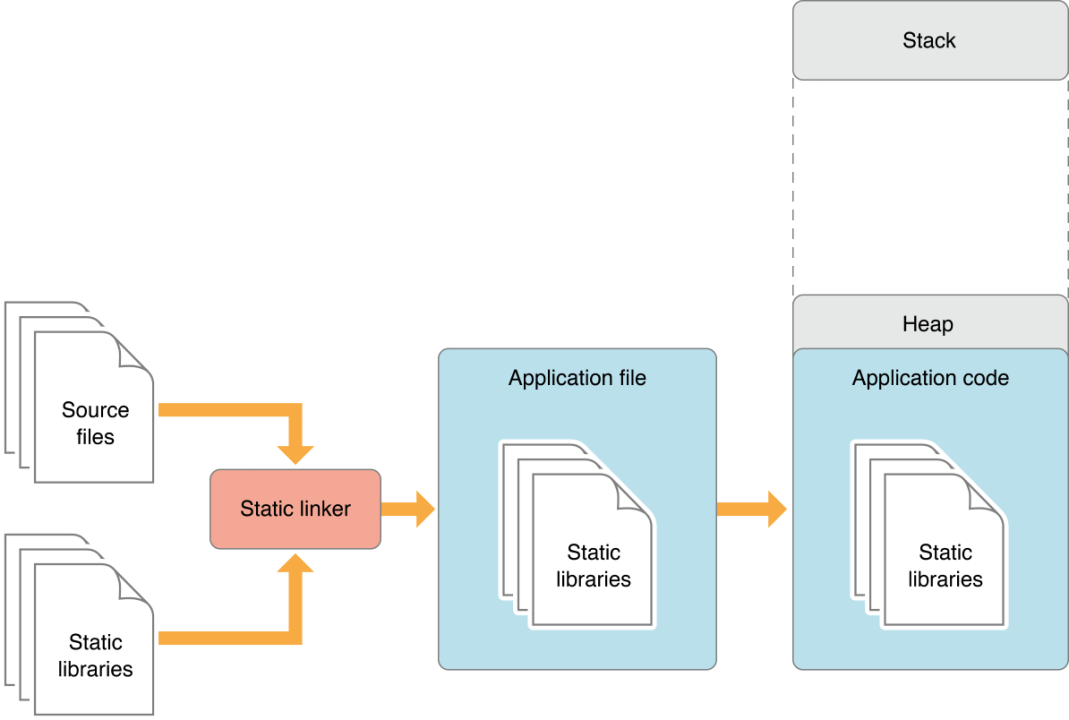
A software engineer like me had just written a C code and passed the code's source file to gcc compiler by executing the command "gcc main.c" on his computer. This action instructs the computer to use gcc compiler to compile his C codes. The process begins with the processor grabbing the C code, otherwise known as the "source file" and removes any comments, macros and expands included files (if any) into the source file. The pre-processed output is stored in the .i file, for example main.i, i.e. a filename ending with .i extension. This stage is known as "per-processing stage".

Compiler Stage

The second stage is the compiling stage, where the .i file is compiled to produce an intermediate compiled output file with .s extension, for example main.s. This file is in assembly level instructions; it contains assembly language codes. This is so because the next stage is the assembly and this is the language the assembler can understand.

Assembly Stage

In assembly stage, the assembly codes with a .s file extension is taken as input and turned into object codes with .o file extension by the assembler. For example main.o. This .o file contains machine level instructions. At this stage, only existing code is converted into machine language, the function calls like printf() are not resolved.

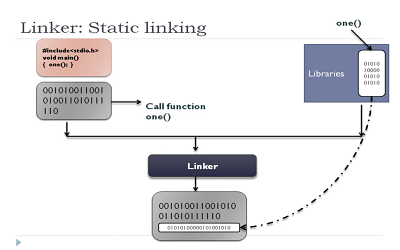
Linker Stage

The last stage is called the linking stage and this is the final phase in which all the linking of the object files, libraries and function calls with their definitions are done. The linker does extra work, it pulls together all the function calls and their definitions with libraries and link them up to create an executable file. It may add extra codes where necessary. The executable file created has a .exe file extension, for example hello_world.exe and can be executed by the computer to generate human readable information.

That is all that there is to it.

Happy coding. Enjoy!